Problème du rendu de monnaie
Introduction
Objectif
L'objectif de ces travaux pratiques est de comprendre et mettre en oeuvre un algorithme glouton.
Préparation
Afin de garder organisées les productions réalisées en travaux pratiques, veuillez mettre à jour l'arborescence du dossier NSI en fonction l'ordinateur utilisé :
💻 Ordinateur portable
- Lancer l'explorateur de fichiers
- Se rendre dans le dossier Documents
- Créer le dossier NSI s'il n'existe pas
- Dans le dossier NSI, créer le dossier chapitre_16
- Dans le dossier chapitre_16, créer le dossier tp1_monnaie
🖥 Ordinateur fixe des salles informatiques
- Depuis le bureau, cliquer sur l'icône intitulée Zone personnelle
- Créer le dossier NSI s'il n'existe pas
- Dans le dossier NSI, créer le dossier chapitre_16
- Dans le dossier chapitre_16, créer le dossier tp1_monnaie
Cours
Optimisation combinatoire
Un problème d'optimisation consiste à déterminer le minimum ou le maximum d'un objectif défini sur le problème. Quelques exemples :
- On dispose d'un réseau routier et on recherche la distance minimale en kilomètres entre deux nœuds A et B du réseau ;
- On dispose d'un système monétaire avec des pièces de 1, 2, 5, 10, 20, 50, 100 unités monétaires et on veut déterminer pour une somme quelconque le nombre minimal de pièces qui permettent de constituer cette somme ;
- On dispose d'un sac à dos d'une capacité maximale en volume et d'une liste d'objets (non fractionnables) de valeur et de volume donnés et on veut déterminer la sélection d'objets permettant d'optimiser la valeur globale du sac tout en respectant la contrainte de capacité.
Les situations données en exemple constituent des problèmes d'optimisation combinatoire. C'est-à-dire qu'il est possible de déterminer une solution exacte par une méthode d'énumération exhaustive, dite de force brute. Autrement dit, la recherche de la solution s'effectue en testant toutes les combinaisons possibles, comme lorsqu'il s'agit de retrouver le code secret d'un cadenas.
En procédant ainsi, on se heurte cependant rapidement à une croissance exponentielle du nombre de solutions possibles en fonction de la taille du problème.
L'algorithme glouton
Pour certains problèmes d'optimisation, un algorithme glouton permet de construire plus efficacement une solution exacte ou du moins, d'avoir une solution approchée acceptable.
Un algorithme glouton construit une solution au problème d'optimisation avec une approche descendante, réduisant progressivement le problème initial par une succession de meilleurs choix locaux :
- On choisit le meilleur candidat parmi les choix disponibles en appliquant toujours le même critère
- On ne remet jamais en cause les choix précédents
Efficacité et limite
Un algorithme glouton est efficace car il progresse directement vers une solution sans jamais revenir en arrière.
Néanmoins, pour que la solution construite soit exacte, il faut que les choix successifs d'optimums locaux conduisent à la réalisation d'un optimum global. Ce n'est pas forcément vrai comme le prouve cet exemple où le choix glouton du plus proche voisin à partir du nœud A (10 + 5) ne conduit pas au plus court chemin (14) de A vers C :
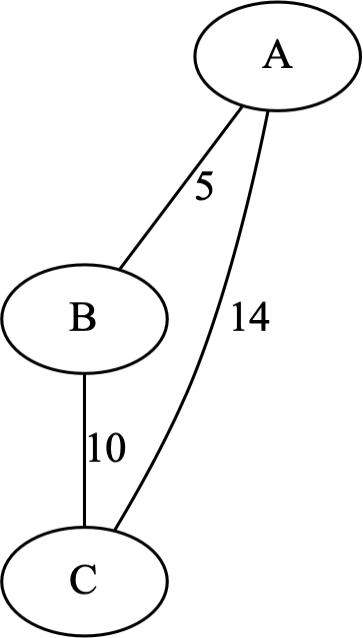
Problème du rendu de monnaie
Présentation
Un achat dit en espèces se traduit par un échange de pièces et de billets. Pour simplifier, considérons que les pièces désignent indifféremment les véritables pièces ou les billets. Supposons qu'un achat induise un rendu de monnaie 49 euros. Quelles pièces peuvent être rendues ? La réponse n'est pas unique :
- Quatre pièces de 10€ 1 pièce de 5€ et deux pièces de 2€ conviennent.
- Mais quarante-neuf pièces de 1€ conviennent également !
Si la question est de rendre la monnaie avec un minimum de pièces, la réponse reste simple : c'est la première solution proposée. Toutefois, comment parvient-on à un tel résultat ? Quels choix ont été faits qui optimisent le nombre de pièces rendues ?
Le problème est de rendre la monnaie en un minimum de pièces.
Algorithme glouton
Système monétaire européen
Faire l'exercice 1 de la fiche activité 1
Autre système monétaire
On considère maintenant le système monétaire systeme = [1, 3, 6, 12, 24, 30].
Quelle est la solution gloutonne pour un rendu de monnaie de 49€ ? Est-elle optimale ?
Un système monétaire pour lequel l'algorithme de rendu de monnaie glouton donne toujours un nombre minimal de pièces est dit canonique. Il existe des algorithmes permettant de déterminer si un système monétaire est canonique.
Algorithme
Faire l'exercice 2 de la fiche activité 1 :
- Écrire l'algorithme
- L'implémenter en Python