Conversion base 2 ↔ base 10

👨‍🏫 Introduction

Objectif

Implémenter en Python des fonctions de conversion entre la base 2 et la base 10.

Important

Les productions réalisées dans le cadre de ce TP seront à rendre en fin de séance :

• Envoyer obligatoirement vos fichiers sous forme d'une archive au format ZIP (et non 7zip ou 7z)
• Effectuer le rendu uniquement depuis l'application Exercices de l'ENT, via l'exercice intitulé [5TP1] Rendu inital

Préparation

Afin de garder organisées les productions réalisées en TP, mettre à jour l'arborescence NSI selon l'ordinateur utilisé :

💻 Ordinateur portable

1. Lancer l'explorateur de fichiers
2. Se rendre dans le dossier Documents
3. Créer le dossier NSI s'il n'existe pas
4. Dans le dossier NSI, créer le dossier chapitre_05
5. Dans le dossier chapitre_05, créer le dossier tp1_conversions

🖥 Ordinateur fixe des salles informatiques

1. Depuis le bureau, cliquer sur l'icône intitulée Zone personnelle
2. Créer le dossier NSI s'il n'existe pas
3. Dans le dossier NSI, créer le dossier chapitre_05
4. Dans le dossier chapitre_05, créer le dossier tp1_conversions

Téléchargement des fichiers

Pour effectuer ce TP, il est nécessaire de télécharger certains fichiers :

1. Télécharger le fichier ZIP contenant les fichiers du TP : 📦 télécharger
2. Ouvrir le fichier ZIP
3. Copier/coller tous les fichiers dans le dossier NSI\chapitre_05\tp1_conversions

🧰 Partie 1 - Fonctions utilitaires

Exercice 1 - Littéraux et fonctions Python

Les littéraux numériques

En Python, il est possible d'écrire la valeur d'un nombre en base 2, base 10 et base 16 :

Base	Littéral	Valeur
Base 10	15	15
Base 2	0b1111	15
Base 16	0xF	15

Les fonctions de conversion

Il est possible d'obtenir une chaîne de caractères dans une base précise de n'importe quelle valeur numérique en utilisant les fonctions suivantes :

Fonction	Description
bin	Renvoie, sous forme d'une chaîne de caractères, la représentation en base 2 d'une valeur numérique passée en argument
hex	Renvoie, sous forme d'une chaîne de caractères, la représentation en base 16 d'une valeur numérique passée en argument

🛠 Mise en pratique

Dans la console Python, identifier les commandes permettant de répondre aux points listés ci-après. Les commandes trouvées devront être reportées dans le fichier ex1_conversions.py.

1. Obtenir la valeur décimale du nombre binaire 11111001110 (utiliser le littéral base2 de Python dans la console)
2. Obtenir la valeur binaire du nombre décimal 255
3. Obtenir la valeur décimale du nombre hexadécimal F0
4. Obtenir la valeur hexadécimale du nombre décimal 2000
5. Obtenir la valeur binaire du nombre hexadécimal 0xFF
6. Obtenir la valeur hexadécimale du nombre binaire 101110101100

Remarque

Ces littéraux et fonctions vous seront utiles pour vérifier vos résultats dans le cadre d'exercices de conversions.
Attention, pour la suite du TP, les fonctions Python à produire ne devront contenir aucun appel aux fonctions bin et hex.

Exercice 2 - Chaînes de caractères

Principe

Une chaine de caractères est une séquence constituée d'un ou plusieurs caractères. Une séquence est un type de donnée dont les éléments sont individuellement accessibles grâce à leur position appelée indice. Soit la chaîne de caractère "Python" :

À partir de la représentation de cette chaîne de caractères, répondre (mentalement) aux questions suivantes :

• Quelle est la taille de la chaîne de caractères ?
• Quelle est le caractère d'indice 3 ?
• Quelle est l'indice du dernier caractère ?

💡 Solution

• La taille de la chaîne de caractères est 6
• Le caractère d'indice 3 est h
• L'indice du dernier caractère est 5 (ou taille de la chaîne - 1)

Expressions Python

Voici quelques expressions propres aux séquences et donc applicables aux chaînes de caractères :

Expression	Description
x in s	Vaut True si la valeur n se trouve dans la séquence s
x not in s	Vaut True si la valeur n ne se trouve pas dans la séquence s
s[i]	Valeur de l'élément d'indice i (l'indice du premier élément étant 0)
len(s)	Longueur de la séquence s

Exemple d'utilisation de ces expressions depuis la console Python pour la chaîne de caractères "Python" :

>>> langage = "Python"
>>> 'w' in langage
False
>>> len(langage)
6
>>> langage[0]
'P'
>>> langage[len(langage)-1]
'n'

🛠 Mise en pratique

1. Tester chacune de ces expressions dans la console Python en utilisant une chaîne de caractères autre que "Python"
2. Une fois ces expressions maîtrisées, ouvrir le fichier ex2_conversions.py
3. Implémenter la fonction afficher_caracteres en respectant la docstring et les doctests

💡 Code Puzzle

Vous êtes en difficulté ? Voici la solution sous forme de puzzle. Reconstituer le code afin d'obtenir la solution : voir le puzzle

↔️ Partie 2 - Conversion base 2 → base 10

Dans le cadre de cette seconde partie du TP, vous devrez développer une fonction de conversion d'une chaîne de caractères représentant un nombre binaire en une valeur de type int.

Exercice 3 - Valeur de chaque rang

Dans un système de numération positionnel, la valeur d'un chiffre varie selon sa position aussi appelée rang. Cette valeur se calcule selon la formule Valeur = Chiffre x Base^Rang

2	5	6
Rang 2	Rang 1	Rang 0
2 x 102	5 x 101	6 x 100
2 x 100	5 x 10	6 x 1
200	50	6

Exemple avec le nombre 256 en base 10

🛠 Mise en pratique

1. Ouvrir le fichier ex3_base2_rangs.py
2. Implémenter la fonction base2_afficher_valeur_rangs en respectant la docstring et les doctests

Remarque

L'exemple donné concernant le nombre 256 est en base 10. Pour cet exercice, il est maintenant question de la base 2.

💡 Code Puzzle

Vous êtes en difficulté ? Voici la solution sous forme de puzzle. Reconstituer le code afin d'obtenir la solution : voir le puzzle

Exercice 4 - Conversion

Pour obtenir la valeur en base 10 d'un nombre en base 2, il suffit de faire la somme de la valeur de chaque rang :

1101₂ = 1x2³ + 1x2² + 0x2¹ + 1x2⁰ = 1x8 + 1x4 + 0 + 1 = 8 + 4 + 1 = 13₁₀

🛠 Mise en pratique

1. Ouvrir le fichier ex4_base2_base10.py
2. En vous inspirant de la fonction base2_afficher_valeur_rangs de l'exercice 3, implémenter la fonction base2_vers_base10 en respectant la docstring et les doctests

↔️ Partie 3 - Conversion base 10 → base 2

Exercice 5 - Conversion

Principe

La conversion en binaire d'un nombre en base 10 peut se faire selon la méthode de la division. Celle-ci consiste à faire des divisions euclidiennes successives par 2 jusqu'à ce que le quotient soit nul. La lecture des restes, du dernier au premier, permet d'obtenir la représentation binaire du nombre.

Voici un exemple de conversion avec le nombre 12₁₀ :

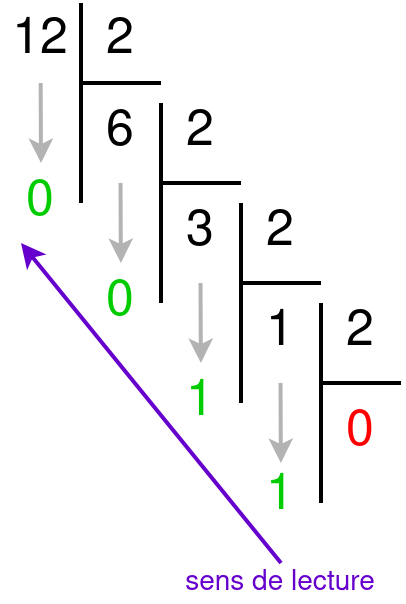
12₁₀ = 1100₂

🛠 Mise en pratique

1. Ouvrir le fichier ex5_base10_base2.py
2. Implémenter la fonction base10_vers_base2 en utilisant la méthode de la division et en respectant la docstring et les doctests

📦 Envoi du travail

Création du fichier ZIP

Pour faciliter le partage de plusieurs fichiers et dossiers, il est de regrouper l'ensemble dans un seul fichier au format ZIP. Lire les instructions selon l'ordinateur utilisés :

💻 Ordinateur portable (Windows 11)

1. Lancer l'explorateur de fichiers
2. Se rendre dans le dossier NSI\chapitre_05\
3. Cliquer une seule fois avec le bouton gauche sur le dossier tp1_conversions pour le sélectionner
4. Cliquer avec le bouton droit sur le dossier tp1_conversions
5. Choisir l'option Compresser dans le fichier ZIP
6. Nommer le fichier nom_prenom_conversions.zip

🖥 Ordinateur fixe des salles informatiques (Windows 10)

1. Lancer l'explorateur de fichiers
2. Se rendre dans le dossier NSI\chapitre_05\
3. Cliquer une seule fois avec le bouton gauche sur le dossier tp1_conversions pour le sélectionner
4. Cliquer avec le bouton droit sur le dossier tp1_conversions
5. Choisir l'option Envoyer vers puis Dossier compressé
6. Nommer le fichier nom_prenom_conversions.zip

Transmission du fichier ZIP

1. Se connecter à l'ENT
2. Accéder à l'application Exercices
3. Cliquer sur l'exercice [5TP1] Rendu inital
4. Choisir le fichier ZIP créé précédemment pour envoi
5. Valider l'envoi du devoir